Mini-Workshop on Celestial Mechanics and Hydrodynamics Finiteness of Central Configuration

报告题目：Finiteness of Central Configurations

报告人：Kuo-Chang Chen

单位：National Tsing Hua University

时间：2023年1月14日09:00-10:20

腾讯会议：567-306-5241

密码：123456

Abstract：Finiteness of central configurations is a long standing open problem. In this talk we will briefly outline some breakthroughs in the past two decades, in particular Hampton-Moeckel’s work for the case n = 4 (Invent. Math. 2006) and Albouy-Kaloshin’s work for the case n = 5 (Ann. Math. 2012). We will report our recent progress for the case n = 6.

报告题目：Finiteness of Stationary Configurations of the Planar Four-Vortex Problem

报告人：Xiang Yu

单位：Southwestern University of Finance and Economics

时间：2023年1月14日10:30-11:50

腾讯会议：567-306-5241

Abstract：For the planar four-vortex problem, we show that there are finitely many stationary con[1]figurations consisting of equilibria, rigidly translating configurations, relative equilibria (uniformly rotating configurations) and collapse configurations. We also provide upper bounds for these classes of stationary configurations. Here, finiteness and upper bounds on collapse configurations are established for each fixed choice of Λ.

报告题目：On the Finiteness of Four-body Central Configurations

报告人：Shuqiang Zhu

单位：Southwestern University of Finance and Economics

时间：2023年1月14日14：00-15：20

腾讯会议：567-306-5241

Abstract：The number of central configurations in the four body problem was proved to be finite, first by Hampton and Moeckel, then by Albouy and Kaloshin, when the masses are all positive. We prove that the four-body central configurations are finite for any four nonzero masses. This is a joint work with Xiang Yu.

报告题目：On the Finiteness of Relative Equilibria of Four Bodies in Homogeneous Potentials

报告人：Julius Natrup

单位：University of Augsburg

时间：2023年1月14日15：30-16：50

腾讯会议：567-306-5241

Abstract：Using BKK theory, we found an upper bound on the number of nondegenerate relative equilibria on any potential of the form 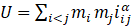 in the case 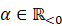 . Using the above result, we could exclude a potentially infinite number of degenerate relative equilibria for almost all 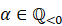 , concluding that there are only finitely many nondegenerate relative equilibria of any such potential as long as 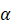    is a negative integer This is joint work with Wang Q. and Wang Y.